M3.1011 Induzione

Pubblicato il 4 marzo, 2011 da bobcarr

Alcuni problemini sull’induzione.

Dimostrare, usando il principio di induzione matematica, le seguenti formule:

  1. n < 2^n \quad \forall n >0
  2. \displaystyle \frac{1}{1^2} + \frac{1}{2^2} + \cdots +\frac{1}{n^2} \leq 2 - \frac{1}{n} \quad \forall n>1
  3. 1^3 + 2^3 + \cdots + n^3 = [\frac{n(n+1)}{2}]^2 \quad \forall n>0
  4. 1 \cdot 2 + 2 \cdot 3 + \cdots + n \cdot (n+1) = \frac{n(n+1)(n+2)}{3} \quad \forall n>0
  5. 2^n < n! \quad \forall n>3
  6. Dimostrare che ogni lettera può essere affrancata con francobolli da 4 e da 5 cent a condizione che costi più di 11 cent.

E vai.

Questa voce è stata pubblicata in Esercizi, Induzione, M3, M3.1011, Matematica, Successioni e contrassegnata con , , , . Contrassegna il permalink.

10 risposte a M3.1011 Induzione

  1. bobcarr ha detto:
    18 marzo, 2011 alle 18:15

    @davecaster

    ottimo, penso tu ti sia guadagnato un k-credito
    però, come faccio a sapere che è tutta farina del tuo sacco?

    Rispondi
  2. davekaster ha detto:
    16 marzo, 2011 alle 18:06

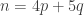
    6. n = 4p + 5q \forall n > 11 \wedge p,q \in N

    n=12

    12 = 4*3 + 5*0 \surd

    Ipotesi Induttiva

    n = 4p + 5q \forall n > 11 \wedge p,q \in N

    n + 1 = 4p + 5q + 1

    p > 0 :

    n+1 = 4p + 5q -4 + 5

    n+1 = 4(p-1) + 5(q+1) \surd

    p=0 :

    n+1 = 4p + 5q + 16 - 15

    n+1 = 4(p+4) + 5(q-3) \surd

    Penso sia dimostrato, dato che da n riesco a ricavare n+1..

    Rispondi
  3. bobcarr ha detto:
    16 marzo, 2011 alle 16:27

    @davekaster

    bene, manca l’ultimo

    Rispondi
  4. davekaster ha detto:
    15 marzo, 2011 alle 23:59

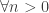
    4. \displaystyle 1*2+2*3+. . .+n(n+1) = \frac{n(n+1)(n+2)}{3} \forall n > 0

    n=1

    2 = \displaystyle \frac {1*2*3}{3} = 2 \surd

    Ipotesi induttiva:

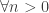
    \displaystyle 1*2+2*3+. . .+n(n+1) = \frac{n(n+1)(n+2)}{3} \forall n > 0

    \displaystyle 1*2+2*3+. . .+n(n+1)+(n+1)(n+2) = \frac{n(n+1)(n+2)}{3}+(n+1)(n+2)

    \displaystyle 1*2+2*3+. . .+n(n+1)+(n+1)(n+2) = (n+1)(n+2) \left(\frac{n}{3}+1\right)

    \displaystyle 1*2+2*3+. . .+n(n+1)+(n+1)(n+2) = (n+1)(n+2) \left(\frac{n+3}{3}\right)

    \displaystyle 1*2+2*3+. . .+n(n+1)+(n+1)(n+2) = \frac{(n+1)(n+2)(n+3)}{3} \surd

    Rispondi
  5. davekaster ha detto:
    15 marzo, 2011 alle 23:49

    3. \displaystyle 1^3+2^3+. . .+n^3 = \left[\frac{n(n+1)}{2}\right]^2 \forall n > 0

    n=1

    1 = \displaystyle (\frac {1*2}{2})^2 = 1 \surd

    Ipotesi induttiva:

    \displaystyle 1^3+2^3+. . .+n^3 = \left[\frac{n(n+1)}{2}\right]^2 \forall n > 0

    \displaystyle 1^3+2^3+. . .+n^3 + (n+1)^3= \frac{n^2(n+1)^2}{4} + (n+1)^3

    \displaystyle 1^3+2^3+. . .+n^3 + (n+1)^3= (n+1)^2 * \left(\frac{n^2}{4} + (n+1)\right)

    \displaystyle 1^3+2^3+. . .+n^3 + (n+1)^3= (n+1)^2 * \left(\frac{n^2+4n+4}{4}\right)

    \displaystyle 1^3+2^3+. . .+n^3 + (n+1)^3= (n+1)^2 * \left(\frac{(n+2)^2}{4}\right)

    \displaystyle 1^3+2^3+. . .+n^3+(n+1)^3= \left[\frac{(n+1)(n+2)}{2}\right]^2 \surd

    Rispondi
  6. davekaster ha detto:
    15 marzo, 2011 alle 16:57

    2. \displaystyle \frac{1}{1^2}+\frac{1}{2^2}+. . .+\frac{1}{n^2} \leq 2-\frac{1}{n} \forall n > 1

    n=2

    \displaystyle \frac{1}{1^2}+\frac{1}{2^2}\leq 2-\frac{1}{2}

    \displaystyle \frac{5}{4}\leq \frac{3}{2} \surd

    Ipotesi induttiva:

    \displaystyle \frac{1}{1^2}+\frac{1}{2^2}+. . .+\frac{1}{n^2} \leq 2-\frac{1}{n} \forall n > 1

    \displaystyle \frac{1}{(n+1)^2} \leq \frac{1}{n} - \frac{1}{n+1} \Leftarrow Lemma 1

    \displaystyle \frac{1}{1^2}+\frac{1}{2^2}+. . .+\frac{1}{n^2}+\frac{1}{(n+1)^2} \leq 2-\frac{1}{n}+\frac{1}{n}-\frac{1}{n+1}

    \displaystyle \frac{1}{1^2}+\frac{1}{2^2}+. . .+\frac{1}{n^2}+\frac{1}{(n+1)^2} \leq 2-\frac{1}{n+1} \surd

    Lemma 1:

    \displaystyle \frac{1}{(n+1)^2} \leq \frac{1}{n} - \frac{1}{n+1}

    \displaystyle \frac{1}{(n+1)^2} + \frac{1}{n+1} -\frac{1}{n} \leq 0

    \displaystyle \frac{n+n^2+n-n^2-2n-1}{n(n+1)^2} \leq 0

    \displaystyle \frac{-1}{n(n+1)^2} \leq 0

    \displaystyle \frac{1}{n(n+1)^2} \geq 0

    Studio i segni:

    \displaystyle (n+1)^2 > 0 \forall n \neq -1

    \displaystyle n > 0

    Quindi : n > 0

    E dato che nell’ipotesi le condizioni erano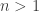 n > 1 , il teorema è dimostrato!

    Rispondi
    • bobcarr ha detto:
      15 marzo, 2011 alle 18:25

      ottimo.

      osservazione: è superovvio che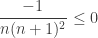 \displaystyle \frac{-1}{n(n+1)^2} \leq 0
      o no?

      Rispondi
      • Edoardo Bastianetto ha detto:
        15 marzo, 2011 alle 18:48

        Il formula dice che n>1 quindi il denominatore è positivo, quindi la frazione e negativa quindi è minore di 0.

        Provando a fare la quarta, a un certo punto si ottiene una formula (A) invece di arrivare alla formula del teorema(B) da quella(A) raccogliendo, si può scomporre la formula B fino a ottienere la formula A? Perchè così si evita di fare ruffini..

        Rispondi

Scrivi una risposta a davekaster Cancella risposta