M3.0809 Disequazioni (ancora?)

Pubblicato il 20 aprile, 2009 da bobcarr

Qualche esercizio in preriscaldamento per la prossima verifica di recupero:

  1. 20 \ln^2 x +31 \ln x -9 > 0
  2. \log_{x^2} (2+x) < 1
  3. (\log_x 2)(\log_{2x} 2)(\log_2 4x)>1
  4. \log_3 \frac{|x^2-4x|+3}{x^2+|x-5|} \geq 0

Buon lavoro.

P.S.

risultati corretti immediati = saranno premiati

Questa voce è stata pubblicata in Disequazioni, Esercizi, esponenziali logaritmi, M3.0809, Matematica e contrassegnata con , , , , . Contrassegna il permalink.

28 risposte a M3.0809 Disequazioni (ancora?)

  1. Andrea Vigani ha detto:
    20 agosto, 2009 alle 19:13

    Salve prof….volevo chiedere una cortesia…se potrebbe per favore postare alcuni esercizi sulla goniometria per tutti i rimandati in matematica,in modo da capire cosa ci aspetta….faccio appello alla sua immensa gentilezza….arrivederci e grazie

    Rispondi
  2. Andrea Vigani ha detto:
    27 Maggio, 2009 alle 16:59

    ***********************************************************
    ************* PER VERIFICA GONIOMETRIA***********************
    ***********************************************************
    Siamo io,Franceschetto e Giachetto in seria difficoltà…
    -Come si risolve l’eq seguente: cos x + cos 3x < 0 ????
    -Cosa intende per equazioni ed disequazioni base?perchè non siamo sicuri che la classe sappia a cosa stiamo andando incontro…
    -Sarebbe possibile spostare la verifica a sabato?
    -Potrebbe mettere un fac-simile del compito qio sul blog?

    Facciamo appello alla sua nota clemenza e bontà…siamo disperati…necessitiamo di aiuto….

    Rispondi
  3. Andrea Vigani ha detto:
    14 Maggio, 2009 alle 16:51

    ***********************************************************
    ************* PER VERIFICA GEOMETRIA ANALITICA ****************
    ***********************************************************
    Prof,
    1.nel compito ci verrà chiesto anche di calcolare il coefficente angolare??
    2.mi potrebbe chiarire la consegna del seguente esercizio che non mi è molto chiara?:
    Problema 28
    Scrivere l’equazione della retta passante per A(–5,–1) parallela alla retta congiungente l’origine delle coordinate con B(1,2).
    P.S. Cosa si intende per: la retta congiungente l’origine delle coordinate???

    Rispondi
  4. Stefano Franceschetto ha detto:
    1 Maggio, 2009 alle 21:21

    Mi vengono tutti tranne la terza..:(

    Rispondi
  5. Giachetto Andrea ha detto:
    1 Maggio, 2009 alle 18:20

    prof ho una domanda.Ma quando la x si trova alla base del log(log di x) devo escludere dalle C.E. anche gli x minori di zero???e devo studiare i due casi in cui la x è compresa fra 0 e 1,e magiore di uno giusto??scusi il disturbo e grazie in anticipo..buon 1 maggio!!!

    Rispondi
  6. bobcarr ha detto:
    30 aprile, 2009 alle 20:45

    Per i lettori affezionati di questo blog: mi è venuta un’idea: rivedete con cura tutti gli esercizi sulle disequazioni logaritmiche/esponenziali pubblicate nei vari post;

    certamente la prossima verifica prenderà da lì.

    Geniale no?

    Rispondi
  7. bobcarr ha detto:
    30 aprile, 2009 alle 20:37

    Es. N.4

    C.E.
    L’argomento del log è una frazione che non può chiaramente mai essere negativa e neanche nulla (il numeratore è minimo 3)
    quindi il C.E. è tutto R.

    Scrivendo 0 come \log_3 1 e passando all’argomento del log, abbiamo:
    \displaystyle \frac{|x^2-4x|+3}{x^2+|x-5|} \geq 1

    dato che il denominatore è sempre positivo, possiamo moltiplicare per il denominatore entrambi i membri e ottenere:

    |x^2-4x|+3 \geq x^2 +|x-5|

    dobbiamo studiare il segno del contenuto dei due moduli e ricavare le zone in cui suddividere la discussione:

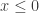    il primo modulo è positivo per x^2-4x \geq 0 e quindi x \leq 0 e x \geq 4

    il secondo x \geq 5

    combinando le varie zone abbiamo in totale 3 sistemi equivalenti; il primo:

    per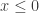 x \leq 0 e 4 \leq x \leq 5
    si ha
    x^2-4x+3 \geq x^2-x+5

    che risolto mi da

    x \leq -\frac{2}{3}

    il secondo per 0 \leq x \leq 4
    -x^2 +4x+3 \geq x^2-x+5

    che risolto mi da

    \frac{1}{2} \leq x \leq 2

    il terzo per x \geq 5 non da alcuna soluzione

    da cui il risultato.

    Buon primo maggio a tutti (i lavoratori).

    Rispondi
  8. Riccardo Lucchetta ha detto:
    30 aprile, 2009 alle 16:52

    Buongiorno prof
    Potrebbe scrivere il risultato della 4?
    A me risulta:
    x<(-1-sqr21)/2

    Rispondi
  9. Alessio ha detto:
    27 aprile, 2009 alle 22:55

    Esercizi di terza o quarta??…Li so fare anche io:) (almeno questi!)

    Rispondi
  10. Giachetto Andrea ha detto:
    27 aprile, 2009 alle 16:51

    il risultato dell es 3. è 1/2<x2????

    Rispondi
  11. bobcarr ha detto:
    23 aprile, 2009 alle 17:26

    Soluzione problema 2) (mica male)

    C.E.

    per via della base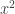 x^2

    x \neq 0 \quad x \neq \pm 1

    2+x > 0
    x > -2

    trasformando il secondo membro abbiamo:

    \log_{x^2}(2+x) < \log_{x^2} x^2

    dobbiamo togliere il log ma si presentano due casi a seconda che la base sia maggiore o minore di 1:

    caso x^2 > 1 cioè
    x < -1 \quad x > 1

    2+x < x^2
    x^2-x-2 > 0 che risolta
    x < -1 \quad x > 2 che intersecata con l’intervallo sopra:

    x < -1 \quad x > 2 che intersecata con il C.E. mi dà
    -2 < x < -1 \quad x > 2

    caso x^2 <1 cioè
    -1 < x < 1

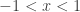
    cambia verso la disequazione

    2+x > x^2
    x^2-x-2 <0
    che risolta mi dà
    -1 < x < 2 che intersecata con la condizione sopra
    -1 < x < 1

    quindi, riassumendo tutte le soluzioni:

    -2 < x < 1 \quad x > 2 ma x \neq 0 \quad x \neq \pm 1

    bello no?

    Rispondi
  12. bobcarr ha detto:
    23 aprile, 2009 alle 16:58

    Problema n. 1)

    C.E. x > 0

    poniamo ln x = y

    20 y^2+31 y -9 > 0

    \ln x < -\frac{9}{5} \quad \ln x > \frac{1}{4}

    0 < x < e^{-\frac{9}{5}} \quad x > e^{\frac{1}{4}}

    fine

    Rispondi
  13. Teso A ha detto:
    22 aprile, 2009 alle 20:21

    1) 0<x e alla 1/4
    2) -1<x<2 e x diverso da 1
    Scusi prof ma il latex non l’ho ancora imparato….sono corretti?

    Rispondi
  14. Andrea Vigani ha detto:
    20 aprile, 2009 alle 15:20

    es.1

    ln(x) 1/4 ……C.E. X>0

    Rispondi
  15. Andrea Vigani ha detto:
    20 aprile, 2009 alle 15:18

    es.2

    x>1 ( x maggiore di 1)

    Rispondi

Lascia un commento