M4.1112 Complessi 8

Pubblicato il 24 novembre, 2011 da bobcarr

In preparazione all’evento:

a) Semplificare e trasformare in forma esponenziale (utilizzare eventualmente la formula di De Moivre):

  1. \displaystyle \left ( \frac{1+ \sqrt{3}i}{1-\sqrt{3}i} \right )^9
  2. \displaystyle \left ( \frac{-1 + \sqrt{3}i}{2} \right )^5 + \left ( \frac{-1- \sqrt{3}i}{2} \right )^5
b) Calcolare le radici complesse:
  1. \displaystyle \sqrt[3]{1}
  2. \displaystyle \sqrt[4]{1}
  3. \displaystyle \sqrt[5]{1}
  4. \displaystyle \sqrt[3]{-1}
  5. \displaystyle \sqrt[4]{-1}
  6. \displaystyle \sqrt[5]{-1}
c) Risolvere le equazioni a coefficienti complessi:
  1. \displaystyle (z-1)^3 +i=0
  2. \displaystyle z^6-64=0
  3. \displaystyle (z+i)^3 = \frac{1-i}{1+i}
  4. \displaystyle z^4+z^2-2=0
Non riesco a capire bene come si risolve questo esercizio:
d) Determinare le radici seste complesse di 1, sia in forma esponenziale che in forma algebrica; calcolare poi (1-i)^6 e dedurre da ciò le radici seste di 8i.
? chi sa come si risolve?
\ Frac
Questa voce è stata pubblicata in equazioni, Equazioni algebriche, M4, Matematica, Numeri complessi e contrassegnata con , , , . Contrassegna il permalink.

18 risposte a M4.1112 Complessi 8

  1. edoardobastianetto ha detto:
    3 dicembre, 2011 alle 15:55

    b) 3.

    \sqrt[5]{1}=\sqrt[5]{1+0i}=\sqrt[5]{e^{i(2 \pi+2k \pi)}}

    e^{i(2 \pi+2k \pi)^\frac{1}{5}}

    Uso formula di De Moivre

    e^{i(\frac{2}{5} \pi+\frac{2}{5}k \pi)}

    Soluzioni:

    e^{i \frac{2}{5} \pi}

    e^{i \frac{4}{5} \pi}

    e^{i \frac{6}{5} \pi}

    e^{i \frac{8}{5} \pi}

    e^{i2 \pi}

    Rispondi
  2. Riccardo Pasianotto ha detto:
    1 dicembre, 2011 alle 19:30

    Dopo un breve ripasso latex, e dopo un gran bel periodo di assenza,

    Posto le soluzioni b.2)
    z_0 = i
    z_1 = -1
    z_{2,3} = 1

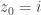
    Spero siano corrette.

    Rispondi

  4. Pingback: Matematica 5/12/11 « Sapere è Potere

  5. ahmedkouza ha detto:
    30 novembre, 2011 alle 17:56

    \displaystyle (z-1)^{3} +i=0
    \displaystyle (z-1)^{3} -i^{3}=0
    \displaystyle (z-1-i)(z^{2}+(i-2)z-i)=0
    prima soluzione:
    \displaystyle z_{1}=1+i
    seconda e terza soluzione:
    \displaystyle z_{2,3}=\frac{2-i \pm \sqrt{3}}{2} = \pm \frac{\sqrt{3}}{2} - \frac{1}{2}i+1

    Rispondi
  6. edoardobastianetto ha detto:
    30 novembre, 2011 alle 17:56

    A) 1.

    \displaystyle (\frac{1+\sqrt{3}i}{1-\sqrt{3}i})^9

    razzionalizzando

    \displaystyle (\frac{-1+\sqrt{3}i}{2})^9

    il modulo si vede che è 1

    \displaystyle arctan(-\sqrt{3})

    f.trigonometrica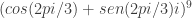 \displaystyle (cos(2pi/3)+sen(2pi/3)i)^9

    trasformiamo in trigonometrica

    \displaystyle {e^({i2pi/3}})^9

    \displaystyle {e^{i18pi/3}}

    \displaystyle {e^{i6pi}}

    \displaystyle e^{i2pi}

    (1)

    Rispondi
  7. Matteo Alessandrini ha detto:
    25 novembre, 2011 alle 16:14

    Ci provo..
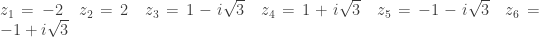
    Soluzione eq numero 2:
    \displaystyle z_{1}=-2 \quad z_{2}=2 \quad z_{3}=1-i\sqrt{3} \quad z_{4}=1+i\sqrt{3} \quad z_{5}=-1-i\sqrt{3} \quad z_{6}=-1+i\sqrt{3}
    Soluzione eq numero 4:
    \displaystyle z_{1}=+1 \quad z_{2}=-1 \quad z_{3}=-i\sqrt{2} \quad z_{4}=+i\sqrt{2}

    Ne ho fatte altre nella sezione “Calcolare le radici complesse”, ma non sono sicuro che il Latex me le prenda tutte in una volta. Potremo correggerle in classe?

    Rispondi

Scrivi una risposta a bobcarr Cancella risposta